Did atmospheric thermal tides cause a daylength locking in the Precambrian? A review on recent results

Abstract

After the initial suggestion by Zahnle and Walker (1987) that the torque accelerating the spin rate of the Earth and produced by the heating of the atmosphere by the Sun could counteract the braking luni-solar gravitational torque in the Precambrian, several authors have recently revisited this hypothesis. In these studies, it is argued that the geological evidence of the past spin state of the Earth plays in favor of this atmospheric tidal locking of the length of the day (LOD). In the present review of the recent literature, we show that the drawn conclusions critically depend on LOD estimates based on stromatolite growth band data of Panella at 1.88 and 2.0 Ga which are subject to large uncertainties. When only the most robust cyclostatigraphic estimates of the LOD are retained, the LOD locking hypothesis is not supported. Moreover, our consideration of the published General Circulation Model numerical simulations and of a new analytical model for the thermal atmospheric tides suggest that the atmospheric tidal resonance, which is the crucial ingredient for the LOD locking in the Precambrian, was never of sufficiently large amplitude to allow for this tidal LOD lock.

Lay summary

Due to tidal interaction between the Earth and the Moon, dissipation occurs, slowing Earth's rotation while causing the Moon to move away from the Earth at a present rate of 3.8 cm per year. Laser reflectors left by Apollo astronauts on the Moon's surface enable extremely precise measurements of this recession. Meanwhile, rock samples brought back from the same Apollo missions helped estimate the Moon's age at 4.25 Ga. Until recently, no physical model could account for Moon's history from its formation near the Earth to its present position. This gap was filled by a scenario fitting both the age of the Moon and its measured present recession (Farhat et al., 2022). Despite agreement with geological evidence, alternate propositions arose last year. One such hypothesis, a revival of ideas proposed by Zahnle and Walker (1987), suggests Earth’s spin stalled in the Precambrian due to a competition between gravitational and thermal atmospheric tides, decelerating and accelerating Earth’s spin, respectively. Thermal atmospheric tides are currently only a small fraction of the complete tidal pull on Earth, but in the past, they may have increased due to a resonance. To clarify this situation, we provide here an extensive discussion of recent literature and conclude that thermal tides were likely never strong enough to balance gravitational tides.

1. Introduction

Since the work of George Darwin, it is known that the body tides exerted by the Sun and Moon on Earth slow down the spin of the Earth and make the Moon recede away from the Earth (Figure 1) (Darwin, 1879; MacDonald, 1964; Goldreich, 1966; Kaula, 1964; Mignard, 1979, 1980; Hut, 1981; Touma & Wisdom, 1994; Néron De Surgy & Laskar, 1997). More elaborate tidal models take into account the oceanic tides, which also slow down the rotation of the Earth and let the Moon go away from the Earth (Webb, 1982; Green et al., 2017; Tyler, 2021; Daher et al., 2021), but none of these tidal models could fit both the present tidal recession of the Moon of 3.83±0.008 cm/yr (Williams & Boggs, 2016) and the age of the Moon of 4.425±0.025 Ga (e.g., Maurice et al., 2020). Elaborated along the lines of Webb (1982), the recent semi-analytical model of Farhat et al. (2022) provides a coherent scenario for the Earth-Moon tidal evolution, with an excellent fit to the present recession rate and the age of the Moon that were included as constraints on the model. It starts with a global ocean in the ancient eons, and then switches to a hemispheric ocean model similar to Webb (1982), but which follows the continental evolution in the most recent 1 Ga. In order to avoid possible circular arguments, no geological proxies of the Earth-Moon distance evolution were used for the elaboration of the model. Despite this, the new model is in good agreement with such geological estimates of the past Earth-Moon distance, and in particular with the recent values obtained by cyclostratigraphic methods (Figure 2). Nevertheless, following the original suggestion of Zahnle and Walker (1987), two recent papers propose that the spin of the Earth was trapped in a resonance between the thermal atmospheric torque and the solid and oceanic torque during the Precambrian Era (Mitchell & Kirscher, 2023; Wu et al., 2023). They also suggest that this stalling of the Earth’s spin rotation speed is correlated with the so-called boring billion (e.g., Holland, 2006). Both studies advocate that this locking of Precambrian day-length is supported by geological observations. However, such a scenario is incompatible with the Earth-Moon evolution presented in Farhat et al. (2022). In this review, which is aimed to the stratigraphic community, we will explicit the differences in the modelling approaches and discuss the use of geological data that can be compared with the models.

Figure 1. In the Darwin model, the Moon produces a tidal bulge on the Earth, but as the Earth is not totally elastic, this bulge is driven by the fast rotation of the Earth slightly off from the Moon direction (angle δ). This results in a braking torque that slows down the spin of the Earth. By conservation of the angular momentum in the Earth-Moon system, the Moon moves away from the Earth.

Figure 2. Evolution of the length of day (LOD) in the past following the model of Farhat et al. (2022). The nominal LOD values are in purple, with the uncertainty indicated by the blue lines (adapted from Figure 5 of Farhat et al., 2022). The circles represent the available cyclostratigraphic data with their uncertainty, when available, from various sources: references within Farhat et al. (2022) in blue, Zhou et al. (2022) in red, and Zeeden et al. (2023) in orange. Tidal rhythmites values are represented by yellow squares, with references from Farhat et al. (2022) with the addition of a data point at 3.2 Ga from the Moodies Group (Eulenfeld & Heubeck, 2023).

1.1. Atmospheric thermal tides

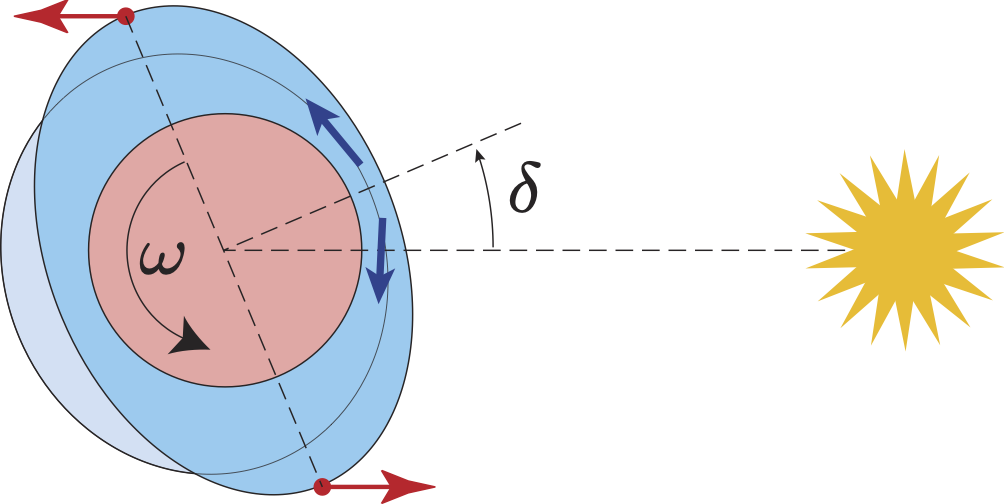
Atmospheric thermal tides have been recognized since the 18th century (see Wilkes, 1949). Due to the heating of the atmosphere by the Sun, the atmosphere locally expands and the pressure decreases at the subsolar point, which induces a redistribution of the mass of the atmosphere, with two main components: a diurnal component, which at equilibrium is opposite to the subsolar point, and a semi-diurnal component, orthogonal to the Sun direction (Figure 3). As for the solid tides, since the Earth spin rotation is faster than its orbital motion around the Sun, the Earth rotation drags these atmospheric bulges with a positive offset from their equilibrium position. At present, the gravitational attraction of the Sun on these bulges induces an accelerating torque, opposite to that of the solid and ocean tides (Chapman & Lindzen, 1970; Goldreich & Soter, 1966; Gold & Soter, 1969; Ingersoll & Dobrovolskis, 1978; Dobrovolskis & Ingersoll, 1980; Correia & Laskar, 2001, 2003; Correia et al., 2003; Leconte et al., 2015; Auclair-Desrotour et al., 2017, 2019).

Figure 3. Thermal atmospheric tides. Due to the heating of the Sun at the subsolar point, a redistribution of the atmosphere creates two main components: a diurnal component (in light blue), and a semi diurnal component (in blue) that are offset from their equilibrium position by an angle δ because of the Earth’s fast rotation speed (ω). They create an accelerating torque on the Earth's spin motion.

1.2. A possible lock of the length of the day

At present, the thermal atmospheric tidal torque is a small part (∼6.4%) of the solid and oceanic tidal friction (Volland, 1990; Farhat et al., 2024), but there are two elements that can change this ratio in favor of the atmospheric thermal tides. First, the atmospheric torque amplitude is dependent on the spin rate of the Earth. As for the oceanic tides, there exists a known resonance of the planetary Lamb wave (Bretherton, 1969), that we name here the Lamb resonance (Farhat et al., 2024), occurring for a faster spin value of the Earth, where the atmospheric torque is largely increased (Lindzen & Blake, 1972; Zahnle & Walker, 1987; Bartlett & Stevenson, 2016). In addition, the oceanic tidal friction is at present close to a resonance, but its value was smaller in the past, for a faster rotation spin value (e.g., Farhat et al., 2022). These elements led Zahnle and Walker (1987) to propose that at some time in the Precambrian, the accelerating thermotidal torque counter-acted the braking luni-solar gravitational tidal torque, which led to a lock of the length of the day (LOD) at about for an extended period of more than 1 Ga. This hypothesis, recently revisited by Bartlett and Stevenson (2016), was probably motivated by the difficulty to fit the existing geological indicators of the past Earth-Moon distance and LOD with more simple models (e.g., Williams, 2000; Hinnov, 2018; Laskar, 2020).

Both in Zahnle and Walker (1987) and Bartlett and Stevenson (2016), a large part of the observational constraints was provided from the Precambrian estimates of the LOD resulting from the analysis of stromatolite deposits (Pannella, 1972a, b) (Figure 4).

Figure 4. LOD locking due to thermal atmospheric tides resonance for the scenarios of Zahnle and Walker (1987) (in red) and Bartlett and Stevenson (2016) (in grey). The geological indicators that are plotted are limited to pre-2016 published results, adapted from Laskar (2020) and Williams (2000) (see references therein). The dotted red line is the LOD provided by equation 41 of Laskar et al. (2004) with a simple Darwin tidal model. The dotted black line is an empirical fit using a simplified tidal model adjusted to the geological data (Walker & Zahnle, 1986). The stromatolite data points at 1.88 and 2.0 Ga are from Pannella (1972a, b).

2. Geological archives for Precambrian LOD estimates

In his review of geological archives for LOD estimates, Williams (2000) mentioned several varieties of bio-archives (bivalves, corals, brachiopods) which we will not consider here, as they were not present in the Precambrian. For these, one can also consult Rosenberg et al. (1975) or Lambeck (1980). We will concentrate here on the stromatolites (2.1), the tidal rhythmites (2.2), and the promising cyclostratigraphic records (2.3).

2.1. Stromatolites

The model of Bartlett and Stevenson (2016) relies heavily on the adjustment to stromatolite data (Pannella, 1972a, b), although the authors themselves warn the reader, and we can quote from Bartlett and Stevenson (2016, p.7): “However, these data, particularly the early stromatolite data (Pannella, 1972), should not be taken too seriously (Zahnle & Walker, 1987). Paleontologists Scrutton(1978) and Hofmann (1973) also found these data to be unreliable and unsuitable for precise quantitative analysis.” These data have also been used in a crucial manner in the recent studies (Mitchell & Kirscher, 2023; Wu et al., 2023; Bao et al., 2022).

Stromatolites are layered organo-sedimentary structures formed by the capture of sediments by microbial organisms, typically formed in shallow marine and lacustrine environments. They are some of the oldest known forms of life, and are an important archive for studying Precambrian paleoenvironments. Studies of recent analogues have shown that daily rhythms of biological growth and binding of sediment can be preserved in stromatolite layering, as the microorganisms (algae) respond actively to daylight (e.g., Logan et al., 1964; Monty, 1967; Davies, 1970; Gebelein, 1969). In addition, environmental fluctuations influence rates of growth and the supply of material, i.e. layering thickness, including tidal and seasonal variations (Gebelein & Hoffman, 1968; Pannella, 1976, 1972b). As such, investigations have been made of diurnal growth layers interpreted from fossil stromatolites that can be structured in larger tidal and seasonal banding; these observations have in turn been used to estimate past LOD and the length of the lunar month. The studies of Precambrian stromatolites by Pannella (1972a, b) are well-known examples that are often used in long-term reconstructions of the past Earth-Moon system (e.g., Bartlett & Stevenson, 2016; Bao et al., 2022; Mitchell & Kirscher, 2023; Wu et al., 2023). The three oldest, most critical LOD data that are often referenced are based on stromatolite sequences from the upper Paleoproterozoic Gunflint Formation (Fralick et al., 2002) and age-correlative Biwabik Formation (Lake Superior region), and the Great Slave Supergroup (Northwestern Territories). However, as emphasized in many studies (e.g., Hofmann, 1973; Scrutton, 1978; Lambeck, 1980), and by Pannella himself in the original publications, these stromatolite-based estimates are rarely, if ever, suitable for precise quantitative interpretation. The formation of daily laminae depends on a fine environmental balance that can easily be disturbed. Stromatolite growth patterns are therefore rarely considered to be complete due to periods of non-deposition and/or post-depositional erosion by for instance storms. For this reason, counts or sequences of laminae should generally be interpreted as minimum estimates, and not as most likely values (Pannella, 1972a, b; Lambeck, 1980). Another source of uncertainty arises from ambiguities associated with determining the exact number of daily laminae per lunar monthly or annual bundle, which is often characterized by a low reproducibility rate.

A lack of internal self-consistency can be noted in the reported growth rhythm hierarchies of the Paleoproterozoic stromatolites studied by Pannella (1972a, b), highlighting the discontinuous nature of the sequences and leaving room for alternative interpretations. More specifically, the counts of the number of diurnal laminae per larger seasonal growth bands yielded a significantly lower interpreted number of days per year than is implied by the observed number of daily increments between lesser growth marks that were believed to indicate the synodic month, obtained from the same sequences. For example, in stromatolites from the ca. 1.88-Ga Gunflint Formation, a maximum of 39 and a mean of 33.4 small-scale laminae were observed per medium-scale growth band interpreted as the synodic month. This ratio implies more than 532 days/year when multiplied by the maximum of 28 observed (and interpreted) fortnightly cycles/year, compared to only 448 diurnal increments that were directly counted within a full seasonal band (Pannella, 1972a). However, for specimens from the time-equivalent Biwabik Formation, Mohr (1975) arrived at a very different growth rhythm hierarchy and conflicting interpretation, suggesting a synodic month of less than 26 days. For the Biwabik Formation, Pannella (1972b) himself counted only 310 diurnal laminae/year directly, while obtaining 442 days/year through extrapolation of interpreted monthly patterns.

Lastly, past LOD estimates based on stromatolites are typically challenged by a lack of (sufficiently precise) independent temporal control on sedimentation/growth rates as well as the absolute age of deposition. This is a challenge that is, however, not unique to the stromatolite archive (tidal rhythmites, for instance, feature similar challenges). Of specific concern here is the uncertainty in the age of the 'Great Slave Supergroup' stromatolite studied by Pannella (1972b). In the literature, this datum point is usually placed around 2 Ga, following the compilation figure of Williams (2000) and given a lack of stratigraphic details provided in (Pannella, 1972b). However, this sample most likely originates from the Pethei Group (Pope & Grotzinger, 2000; Hoffman, 2023, pers. comm.), the current best age constraints of which indicate a significantly younger age between 1.889 and 1.867 Ma (Hoffman et al., 2023). In conclusion, while stromatolites can provide useful insights in past tidal dynamics, they should typically not be considered as providing accurate or precise numerical values for past LOD reconstructions.

2.2. Tidal rhythmites

Tidal rhythmites are laminae deposits related to semi-diurnal or diurnal tidal cycles that can occur in estuaries or deltas. Silty and muddy sediment is carried by ebb tidal currents. These currents transport the sediment in suspension through the main ebb channel to deeper offshore water, where it settles and forms graded layers. During slack water between tides, muddy caps can be deposited on the sandy laminae. The amount of sediment carried by ebb tidal currents, its grain size, and the effectiveness of tides in transporting and depositing sediment, are directly related to the tidal amplitude (Williams, 2000). In an ideal scenario, the analysis of the time series of the thickness of these laminae should allow recovery of all tidal periodicities, such as:

• The lunar day, which is the interval between two passages of the Moon at the meridian.
• The lunar synodic month, which separates two full Moons, and is thus recovered by the recognition of spring tides of large amplitude, occurring at syzygy, when the Moon and the Earth have same longitude as seen from the Sun.
• The tropical year, separating two passages of the Earth at the spring equinox (also called vernal equinox), possibly determined as the time of maximal tidal amplitude in the year.
• Finally, if the record is sufficiently long, the nodal period of the Moon (18.6 yr at present) (Walker & Zahnle, 1986).

Although very promising, this method has its drawbacks. The locations where high-quality sequences of such laminae formations can be observed are rare. Moreover, they often lead to divergent analyses when the deposits are analyzed by different groups. The Weeli Wolli Formation in Western Australia, dated 2.45 Ga, was interpreted by Walker and Zahnle (1986) on the basis of the lunar nodal cycle, and led to a reconstructed Earth-Moon distance of Earth radius , while the analysis of (Williams, 1989,1990 resulted in a much larger value of , with the analysis of laminae couplets, grouped in synodic fortnightly increments, and annual cycles. Although the results of these two studies are still consistent within uncertainty (given the very large error bars), these estimates are based on two fundamentally different and mutually incompatible interpretations of the same layering patterns. In the same way, the analysis of the Elatina Formation in South Australia, dated 620 Ma, led Williams (1989, 1990) to determine an Earth-Moon distance of while Sonett and Chan (1998) derived from their analysis of the same sequence. Sonett and Chan (1998) also re-analyzed their previous determination of the Earth-Moon distance for the Big Cottonwood Formation in Utah, at , and found a value corresponding to an Earth-Moon distance of , while their previous determination of the same sequence was (Sonett et al., 1996). We note that the new determinations from Sonett and Chan (1998) are in agreement with the new model of Farhat et al. (2022) (Figure 2). However, given the difficulties associated with interpreting Earth-Moon parameters from these tidal sequences, additional independent studies should be required to further verify the determination of Sonett and Chan (1998).

2.3. Cyclostratigraphy

Due to the gravitational interactions of the Earth with the other planets, the orbital plane of the Earth is moving in a complex motion composed of a slow rotation (precession of the node) and a composition of nearly periodic motions that make the inclination of the Earth orbital plane oscillate (e.g., Laskar, 2020). This induces an oscillation of the tilt of the Earth (or obliquity, ε) of present amplitude 1.3 degrees around its averaged value. The variation of insolation on the surface of the Earth depends also on the precession of perihelion, and on the variation of eccentricity, which are dominated by the so-called long eccentricity term of 405 kyr period and the short eccentricities of main periods 95 kyr and 124 kyr. Finally, the pull of the Moon and Sun on the equatorial bulge of the Earth induces a slow precessional motion of its spin axis at 50.475838 arcsec/yr that corresponds to a period of about 26 kyr (Laskar, 2020). Neglecting the eccentricity of the Earth and Lunar orbit, and the inclination of the Moon, the lunisolar precession frequency can be expressed as , where is the obliquity and where the precession constant is equation 4.14 from Laskar (2020):

(1) α=3/2 G [(m_⊙/a³_⊙)+(m_M/a³_M)] (E_d0/γ²₀)γ

where G is the gravitational constant, ⊙ refers to the Sun, and M to the Moon, m and a are the masses and semimajor axes, γ the Earth's spin angular velocity, γ₀ its present value, and E_d0 the dynamical ellipticity at present. As a_⊙ can be considered as constant, the precession constant α thus depends mostly on the evolution of a_M and γ, which evolve with time under tidal dissipation (highlighted in bold in equation (1)).

The resulting changes in insolation drive climatic changes on Earth (astronomical climate forcing) that can be recorded in the Earth's sedimentary archive. These sediments can be studied today (e.g., Gradstein et al., 2004, 2012, 2020; Montenari, 2018) and inform us on past astronomical changes.

Over very long timescales, beyond 60 Ma, the planetary orbital motions can no longer be reconstructed with accuracy (Laskar et al., 2011a, b), but for the Earth-Moon evolution, the tidal dissipation will dominate, and a reconstruction of the past evolution of the Earth-Moon distance can still be achieved. The variation of and will induce a change in the precession period that can be imprinted in the sedimentary record (Berger et al., 1992; Meyers & Malinverno, 2018). In a reverse way, the determination of the precession frequency from the sedimentary record, and the use of a dynamical model that will link the semi-major axis to the angular spin velocity of the Earth can allow retrieval of both and . This determination requires a time-scale for the sedimentary record, which can be provided either by absolute radiometric age dating, or by the use of the 405 kyr eccentricity period as a metronome for stratigraphic cycles (see Laskar, 2020 and references therein). In recent years, this technique for determining the past state of the Earth-Moon system has made much progress, and many groups have obtained converging results using various methods for the determination of the precession frequency (e.g., Meyers & Malinverno, 2018; Lantink et al., 2022; Zeeden et al., 2023). Moreover, these data are in good agreement with the tidal model of Farhat et al. (2022) (see Figure 6 of Farhat et al., 2022, and Figure 5 of Zeeden et al., 2023).

Another crucial advantage of cyclostratigraphy, compared to, for example, stromatolites and tidal rhythmites, is the greater potential of independent age control by, for example, radioisotopic geochronology and integrated stratigraphic approaches. Using an integrated stratigraphic approach it is also possible to verify interpretations in time-equivalent sections that should have the same time-dependent astronomical signatures (e.g., Olsen et al., 2019; Sinnesael et al., 2019). The coherence of these sets of data leads us to consider that they are the most robust among the geological proxies for the determination of the past precession frequency of the Earth and determination of Earth-Moon system parameters. It should nevertheless be stressed that these parameters do not have the same status in cyclostratigraphic studies. The only primary quantity determined directly with cyclostratigraphy is the Earth luni-solar precession frequency. The other parameters of the Earth-Moon system (Earth-Moon distance and LOD) are retrieved only through a dynamical model that should not be limited to the Earth-Moon system. Indeed, one should consider the exchange of the angular momentum in the Sun-Earth-Moon system, and also the variation of this angular momentum through various mechanisms, the largest one probably being atmospheric thermal tides, although this latest can be neglected in a first approximation.

Figure 5. Comparison of the data and fit of Mitchell and Kirscher (2023) (black and red lines) with the model of Farhat et al. (2022) (purple curve with uncertainty in blue). As in Figure 2, LOD (in hours) is plotted against age (in Ma). Tidal rhythmites are yellow squares, and cyclostratigraphic data are color circles (light blue with references in Farhat et al. (2022), red from Zhou et al. (2022), and orange from Zeeden et al. (2023)). The stromatolite data from Pannella (1972a, b) are highlighted with a dark green circle while the cyclostratigraphic data from Grotzinger (1986) is circled in light green. Adapted from Figure 2 of Mitchell and Kirscher (2023).

Figure 6. Comparison of the data and fit of Wu et al. (2023) (in black) with the model of Farhat et al. (2022) (purple curve with uncertainty in blue). As in Figure 2, tidal rhythmites are yellow squares, and cyclostratigraphic data are color circles (light blue with references in Farhat et al. (2022), red from Zhou et al. (2022) and orange from Zeeden et al. (2023)). The stromatolite data from (Pannella, 1972a, b) are highlighted with a dark green circle. Note that these data points seem to be misplaced in the Wu et al. (2023) figure reproduced here (see note 1). Adapted from Figure 3 of Wu et al. (2023).

3. Discussion of the recently published results

The solution of Farhat et al. (2022) is in agreement with the most recent determinations of tidal rhythmites (Sonett & Chan, 1998) and with the recent cyclostratigraphic data (Meyers & Malinverno, 2018; Lantink et al., 2022; Zhou et al., 2022; Zeeden et al., 2023) (Figure 2). One could thus think that the fate of the thermal tides locking hypothesis was settled. However, the recent publication of the two papers (Mitchell & Kirscher, 2023; Wu et al., 2023) in major journals requires some additional discussion to clarify the situation.

3.1. Mitchell and Kirscher (2023)

In their compilation of geological constraints of the Precambrian length of the day, Mitchell and Kirscher (2023) have included most of the available data. Their analysis is purely empirical. They search for the best linear fit, made by pieces over sequences of data. One could wonder on the status of their fit, which is not continuous, as a piecewise linear model would be. The goal is thus not to find an empirical model for the Earth-Moon evolution, but to search for the best fitted trends in the LOD over extended periods. From these fits, they conclude that a LOD lock probably occurred between 1 Ga and 2 Ga. When comparing to the results of Farhat et al. (2022) (Figure 5), one can observe that the stromatolites data at 1.88 Ga and 2 Ga from Pannella (1972a, b) are essential for the conclusions of Mitchell and Kirscher (2023). If these data, which are questionable as we discuss in section 2.1, are not taken into account, the fit will no longer lead to this locked value of the LOD between 1 and 2 Ga.

By contrast, the cyclostratigraphic point of Grotzinger (1986) is nearly exactly on the Farhat et al. (2022) curve (Figure 5). It should be noted, however, that the datum point of Grotzinger (1986) was not originally given in that paper but was derived by Mitchell and Kirscher (2023). Grotzinger (1986) only proposed that there is eustatic sea-level cyclicity within the Milankovitch frequency band recorded in platform carbonates from the Rocknest Formation, at a scale of 1 – 15 m and possibly of 75 – 100 m or 75 – 200 m. Mitchell & Kirscher (2023) then assumed that a 10 m cycle represents climatic precession and 87.5 m is related to short eccentricity. However, this interpretation is poorly constrained. Due to the large uncertainty of this data point, we should consider this as a simple coincidence, until some new quantitative analysis in the spirit of Meyers and Malinverno (2018) is performed on the same 1.89 Ga Rocknest Formation sample (Mitchell & Kirscher, 2023).

3.2. Wu et al. (2023)

In the recent work of Wu et al. (2023), the authors presented a new analytical model of thermal tides to address the resonant locking hypothesis. The model's free parameters were constrained such that the resulting thermotidal torque drives an LOD history that best fits their compilation of LOD geological proxies. As previously, in Figure 6, we compare Wu et al. (2023) (black curve) with Farhat et al. (2022) (purple curve). Here again, one can see that the model of Wu et al. (2023) relies heavily on the stromatolite data of Pannella (1972a, b) to establish the resonance locking of the LOD¹. Moreover, the Wu et al. (2023) curve misses entirely the new cyclostratigraphic determinations of the Earth-Moon state at 2.46 Ga obtained by Lantink et al. (2022) in Joffre Gorge, Australia.

Wu et al. (2023) elaborated a physical model to support their claims. Moreover, the authors performed a suite of GCM (General Circulation Model) numerical simulations, using the LMD-G (Hourdin et al., 2006) and PlaSim (Fraedrich et al., 2005) GCMs, to infer the Earth's paleo-temperature evolution that is required to generate the constrained history of the thermotidal torque. We dedicate the rest of this section to discuss the details behind the model adopted in Wu et al. (2023) and its predictions.

¹ Note that these data points from Pannella (Pannella, 1972a, b) occur at a different age position in the figures 1 – 3 of Wu et al. (2023), compare to previous LOD com-pilations (e.g., Williams, 2000; Bartlett and Stevenson, 2016; Mitchell and Kirscher, 2023). In particular, we note that the two closely spaced points at ca. 1.63 Ga most likely represent Pannella’s analyses of the time-correlative Gunflint (1972a) and Bi-wabik (1972b) Formations dated at ca. 1.88 Ga (Fralick et al., 2002). However, used literature data were not provided in Wu et al. (2023) to verify this observation.

3.2.1. The modeled gravitational tides: artificial resonances?

The dynamical evolution of the Earth's rotational motion in Wu et al. (2023) is driven by the luni-solar gravitational tidal torque and the solar thermotidal torque. For the former, the authors used the tidal history of Webb (1982), where Laplace's Tidal Equations (the equations describing the tidal response of a shallow fluid layer; LTEs hereafter) were solved semi-analytically over a hemispherical equatorial ocean on the surface of the Earth. While the work of Webb (1982) was seminal in coupling LTEs with the dynamical evolution of the Earth-Moon system, the modeled history of the lunar orbit in Webb (1982) yielded a lunar formation epoch that is incompatible with the geologically constrained lunar age (see Figure 3 of Webb, 1982).

To efficiently remedy the latter discrepancy, Wu et al (2023) tweak the tidal dissipation history of Webb (1982) by normalizing it with a constant factor (Q1), such that the resultant orbital history of the Moon features its proper temporal origin (see their equation 1 and S1). As a byproduct of this modeling choice, the authors have modified the spectrum of oceanic normal modes in such a way that tidal resonances are characterized with artificial amplitudes(see Green et al., 2017; Daher et al., 2021; Farhat et al., 2022).

Though the authors focus on modeling thermal tides, gravitational tides remain the dominant driver of the Earth's rotational evolution, providing the background of the tidal torque upon which the thermotidal counterpart would significantly contribute only in the vicinity of the Lamb resonance. As such, since the authors are constraining the history of the total torque to fit a compilation of geological LOD proxies, an artificially modeled spectrum of gravitational tidal dissipation may yield an artificial spectrum of thermal tides. Namely, the resultant thermotidal history could be characterized by either an artificial timing of the Lamb resonance occurrence, an artificial amplitude of the Lamb resonance, or both.

3.2.2. Atmospheric thermal tides: model limitations

For the thermotidal contribution to the Earth's rotational history evolution, Wu et al (2023) develop a simplified analytical model of thermal tides that is used to compute the thermotidal torque (Equations S28-S29 therein). The model is parameterized by a number of free parameters (16 in total) that are constrained such that the resulting thermotidal torque, added to the gravitational tidal torque, would drive an LOD history that fits the compilation of LOD geological proxies (see Figure 6).

The developed model essentially resembles a band-pass filter, similar to that developed in Bartlett and Stevenson (2016). It ignores the Coriolis force, which may be significant in the case of a fast rotator like the Earth, along with the vertical velocity of tidal waves. The model also assumes an isothermal structure of the atmosphere. This choice is common in the literature of atmospheric dynamics as it simplifies the mathematical framework of the rather complex theory (e.g., Chapman & Lindzen, 1970; Lindzen & Blake, 1972; Auclair-Desrotour et al., 2019). However, for the Earth, atmospheric temperature measurements (e.g., Figures 2.1-2.3 of Pierrehumbert, 2010) show that the massive troposphere (~80% of atmospheric mass) controlling the tidal mass redistribution is characterized by a negative temperature gradient. The latter is in fact closer to an idealised adiabatic profile than it is to an idealised isothermal profile. These modeling choices could deliver inaccuracies in the determination of the resonant period (Farhat et al., 2024). However, this was somewhat compensated by the authors in modeling the resonant period as a free parameter that is constrained by the geological data.

The other essential quantity of interest is the amplitude of the thermotidal torque when the resonance is encountered. The latter is dependent on several variables, of which the least constrained in the case of the Earth is the rate of energy dissipation by the atmosphere. Namely, as the atmosphere is heated by the shortwave incident solar flux and the infrared emission from the ground, it dissipates energy via multiple pathways including radiative cooling and frictional interactions with the surface. As it is difficult to properly model these mechanisms in the analytical theory, energy dissipation is usually modeled by a free parameter (the parameter Q_th in the work of Wu et al., 2023). This unconstrained parameter predominantly controls the amplitude and the spectral width of the resonant thermotidal torque and, consequently, the lifetime of the Lamb resonance and whether it was sufficient to counteract the gravitational tide.

Dissipative radiative transfer and atmospheric cooling, however, can be properly accommodated in GCM simulations. To that end, Wu et al (2023) presents, to date, the first study that uses GCMs to simulate the Lamb resonance specifically for the Earth. Their results, using the two aforementioned GCMs, estimate the dissipation parameter to be Q_th ≃ 100, which would render the maximum amplitude of the torque insufficient for the LOD locking. For the LOD evolution, however, the authors used values of that are one order of magnitude larger (Q_th ≃ 100) such that the thermotidal torque would be sufficient to counteract the gravitational counterpart. Consequently, the used thermotidal torque is amplified by a factor of ~30 relative to its present value². The author's reasoning lies in the need for such a large thermotidal torque so that the LOD proxies, specifically the stromatolites in (Pannella, 1972a, b), can be explained. This brings us back to Section 2.1 in questioning the reliability of this data set as a robust constraint for informing dynamical models, especially when present with evidence from GCMs to the contrary.

² Which means that the amplitude of the surface pressure anomaly is amplified by a factor of ~60 as can be inferred from Farhat et al. (2024).

3.2.3. The asymmetry of the Lamb resonance

An interesting signature of the GCM simulations of the Lamb resonance in Wu et al. (2023) lies in the spectrum of the thermotidal torque shown in their Figure S4. We reproduce this spectrum in Figure 7. The GCM spectrum, shown by the black dots, features an asymmetry in the peaks of the Lamb resonance whereby the two peaks of the torque around the resonance do not share the same amplitude. Namely, the accelerating part of the torque has an amplitude that is almost half that of the decelerating part. The former part is required to occur with a sufficient amplitude such that it counteracts the decelerating gravitational torque, but it appears from this spectrum to be reduced. The authors, however, ignored this signature present in the GCM simulations in favor of the spectrally symmetric Lamb resonance obtained from their analytical model, which is shown by the black curve in Figure 7. Note that the change from an accelerative to a decelerative tidal torque depends on the orientation of the tidally generated atmospheric mass redistribution, and consequently of the tidal bulge, relative to the subsolar point (see Figures 3 and 4 of Farhat et al., 2024 for further detail).

In the recent work of Farhat et al. (2024), the authors propose that such an asymmetry can be obtained if one accounts for the thermal inertia budget in the ground and the lowermost atmospheric layer. Namely, due to the thermal inertia in these layers, the infrared heating of the atmosphere by the ground becomes asynchronous with the incident solar flux. This delayed ground response is shown to be responsible for maneuvering the atmospheric tidal bulge in such a way that creates an amplitude asymmetry between the two peaks. In Figure 7, we show by the red curve how the model of Farhat et al. (2024) can properly explain the spectral asymmetry of the GCM-produced spectrum when taking into account the thermal inertia effects. It is important to note that the reduction of the positive peak of the torque goes hand in hand with the relative contribution of the ground in heating the atmosphere. Namely, the more abundant the greenhouse gases are in the atmosphere, which is predicted for the Precambrian from various geological proxies (see e.g., Catling & Zahnle, 2020), the more the atmosphere would be prone to infrared thermotidal heating, and consequently the more the accelerating thermotidal torque would be reduced.

3.2.4. The temperature problem

One naturally wonders how the discussed modeling limitations carry over to the model predictions. The resulting timing of the Lamb resonance occurrence requires a mean Earth temperature in the Proterozoic of , computed by the authors using the PlaSim GCM (see Figure 7 of Wu et al., 2023). Though a warm climatic interval fits evidence on a Proterozoic glacial gap (e.g., Hoffman et al., 2017), such extreme temperatures are in contrast with geochemical analysis using phosphates (e.g., Blake et al., 2010), geological carbon cycle models (e.g., Sleep & Zahnle, 2001; Krissansen-Totton et al., 2018), numerical results of 3D GCMs (e.g., Charnay et al., 2020), and the fact that solar luminosity was 10-25% lower during the Precambrian (e.g., Gough, 1981). Such extreme temperature estimates would also require elevated amounts of partial pressure of , reaching 200 mbar. This exceeds inferred estimates from various geochemical proxies (see the review by Catling & Zahnle, 2020, and references therein). More importantly, however, this temperature increase will enhance the asynchronous thermotidal heating of the atmosphere by the ground in the infrared, as we describe in Section 3.2.2. The latter would significantly attenuate the peak of the tidal torque near resonance, rendering it insufficient for the LOD locking. The adopted model in Wu et al. (2023) did not account for this feedback effect. Moreover, atmospheric dissipation is also enhanced with the increased temperature, as discussed in Farhat et al. (2024), which has an additional effect of attenuating the resonant amplitude of the torque.

Figure 7. The spectrum of the thermotidal torque as a function of the length of day (LOD) adapted from Figure S4 of Wu et al. (2023). The black dots are simulated using the PlaSim GCM, while the solid black curve shows the prediction of the analytical model of Wu et al (2023). The red curve shows a fit to the GCM results using the analytical model of Farhat et al. (2024), where the physical effects of the delayed thermal response of the ground were taken into account. These effects proved to induce the notable amplitude asymmetry between the peaks around the Lamb resonance. Namely, the accelerating peak of the tidal torque is reduced in amplitude relative to the decelerating peak.

3.3. Bao et al. (2022)

While they do not invoke a thermal tides LOD trapping, Bao et al (2022) try also to reconciliate the LOD history with the Pannella (1972a, b) data. This time, they propose that between 2 Ga and 1.5 Ga, a sudden growth of the Earth core led to a reduction of the spin rate of the Earth. In Figure 8, we have compared their solution with Farhat et al. (2022) (purple curve). In this case again, the scenario depends crucially on the stromatolite data of Pannella (1972a, b). If these data are removed, there is no longer the necessity to search for some peculiar scenario, and it can be recognized that the model of Farhat et al. (2022) fits most of the reliable geological data in a satisfactory manner.

Figure 8. Comparison of the data and fit of Bao et al. (2022) (in solid blue) with the model of Farhat et al. (2022) (purple curve with uncertainty in green). As in Figure 2, tidal rhythmites are yellow squares, and cyclostratigraphic data are color circles (light blue with references in Farhat et al., 2022, red from Zhou et al., 2022, and orange from Zeeden et al., 2023). The stromatolite data from Pannella (1972a, b) are highlighted with a dark green circle. Adapted from Figure 11 of Bao et al. (2022).

3.4. Farhat et al. (2024)

In their recent work, Farhat et al (2024) have revisited the atmospheric thermal tides computations for rocky planets and in particular for the Earth. They have constructed an ab initio model of thermal tides on rocky planets with a neutrally stratified atmosphere³. This feature is a major change with respect to previous models, where closed-form solutions are usually obtained assuming that the atmosphere is isothermal, which is a less realistic assumption for the Earth troposphere (Lindzen & McKenzie, 1967; Chapman & Lindzen, 1970; Lindzen & Blake, 1972; Auclair-Desrotour et al., 2019; Wu et al., 2023). Although both atmospheric structures provide appreciable mathematical simplifications, neutral stratification appears to better capture the negative temperature gradient that characterizes the troposphere of the Earth, which contains most of the atmospheric mass. As the stability of stratification with respect to convection determines the strength of the Archimedean force exerted on fluid particles in the vertical direction, the neutral stratification approximation annihilates the buoyancy effects in the tidal response. The upward travelling internal gravity waves are thus filtered out from the solution, leaving only the horizontal compressibility forces responsible for the propagation of the Lamb wave. Another major change with respect to previous models (Lindzen & McKenzie, 1967; Chapman & Lindzen, 1970; Lindzen & Blake, 1972; Ingersoll & Dobrovolskis, 1978; Dobrovolskis & Ingersoll, 1980; Auclair-Desrotour et al., 2019; Wu et al., 2023) is the consideration of heat absorption near the ground level and heat exchange between the atmosphere and ground that takes into account the thermal diffusive processes in the planetary surface layer. This model allows to obtain a closed-form solution for the frequency-dependent atmospheric tidal torque, and is in agreement with simulations using GCMs, both for Earth-like and Venus-like planets. Specifically, when applied to the Earth, their model predicts a resonant rotational period of 22.8 hr, which is in agreement with a recent analysis of pressure data on global scales (Sakazaki & Hamilton, 2020)⁴, and the GCM prediction of Wu et al (2023). As such, the model predicts the occurrence of the Lamb resonance not in the Precambrian, but in the Phanerozoic, with an amplitude that is insufficient to counteract the luni-solar gravitational tidal torque. This does not exclude the occurrence of the crossing of the resonance, but as the luni-solar gravitational tidal torque remains larger than the thermotidal torque, no LOD trapping can occur. The crossing of the resonance then results only in a small change of the Earth's rotational deceleration: the spin deceleration rate is slightly increased before the resonance, and then reduced to roughly its previous value after the crossing of the resonance.

The Farhat et al. (2024) model depends on two parameters (σ₀, α_A), which are the cooling frequency and opacity parameters, respectively. The frequency σ₀ is the inverse of the timescale associated with energy dissipation, which is assumed to result from radiative cooling in the model. The higher σ₀, the more efficient is energy dissipation. The frequency σ₀ is thus tightly associated to the amplitude of the Lamb resonance, and thus related to the parameter Q_th appearing in Wu et al. (2023). The opacity parameter α_A quantifies the fraction of incident Solar flux that is transferred to the atmosphere in the thermal tidal forcing. Consequently, this parameter takes its values between 0 (no tidal forcing) and 1 (maximum tidal forcing). Other model parameters are related to the atmospheric gas mixture and surface temperature. For the thermotidal torque to cancel the gravitational torque in the Precambrian (and thus the LOD locking to occur in the Precambrian), the (σ₀, α_A) pair needs to be below the associated black solid curve of Figure 9.

The observation of the present thermal atmospheric response and the constraint on the cooling frequency σ₀ deduced from the cooling timescales estimated by Leconte et al. (2015), impose the (σ₀, α_A⁾ pair to be inside the intersection of the two shaded regions, which allows for a narrow parametric area where the Precambrian LOD lock conditions are met. However, Farhat et al. (2024) show that the crossing of the resonance, within the limitations of their analytical model, most probably occurred in the late Paleozoic/early Mesozoic, and not in the Precambrian. In this case, the curve to consider is the dashed line, and the parametric analysis precludes LOD locking (Figure 9).

³ A neutrally stratified atmosphere is an atmosphere where the temperature and pressure dependance with height is such that the Archimedian restoring forces are cancelled.

⁴ This value is in agreement with the 11.38±0.16 hr semi-diurnal period obtained by analyzing the spectrum of normal modes using pressure data on global scales (see Table 1 of Sakazaki and Hamilton, 2020, first symmetric gravity mode of wav-enumber k = -2).

Figure 9. Amplitude of the Lamb resonance with respect to the two parameters σ₀ and α_A of the Farhat et al. (2024) model. In order for the thermotidal response to cancel the gravitational counterpart in the Precambrian the parameters (σ₀, α_A) need to be below the solid black line. The dashed line defines the same threshold needed for the late Paleozoic/early Mesozoic (350-250 Ma). The horizontal shaded area corresponds to typical values of the radiative cooling rate σ₀. The other shaded area defines the region of parameter space corresponding to the presently observed semi-diurnal tidal bulge. Adapted from Farhat et al. (2024).

4. Conclusions

The famous astronomer Carl Sagan (1934-1996) used to say that extraordinary claims require extraordinary evidence, which is another version of the Occam's razor in science, stating that simpler explanations should be preferred to more complicated ones, in absence of strong arguments. Adapted to the present problem of the evolution of the Earth-Moon distance and LOD, it can be expressed as: Do we need a LOD lock by thermal tides to explain the evolution of the Earth-Moon system over its age? Is there strong evidence for a LOD lock in the Precambrian?

The answer to the first question is clearly negative, as the Farhat et al. (2022) model provides a coherent scenario for the tidal history of the Earth-Moon system, without the need of a resonant atmospheric tidal lock.

We have seen also how all papers advocating for a LOD lock by thermal tides (Bartlett and Stevenson, 2016; Mitchell and Kirscher, 2023; Wu et al., 2023), or the alternate scenario of a growing Earth's core (Bao et al., 2022) rely critically on the stromatolite LOD estimates of Pannella (1972a, b).

However, as emphasised by Pannella himself, and by several authors that studied these data afterwards, the validity of the stromatolite-based LOD estimates derived from the Paleoproterozoic Gunflint-Biwabik Formations and Great Slave Supergroup should be questioned (see section 2.1). There is thus at present no reliable geological evidence to support these alternate scenarios. Moreover, Mitchell and Kirscher (2023) presented a cyclostratigraphy-based datum from cyclicities in the 1.9-Ga Rocknest Formation (Grotzinger, 1986) which is not compatible with the stromatolite data of Pannella. In addition, the solution of Wu et al. (2023) complies with the questionable stromatolite data of Pannella (1972a, b) but not with the more reliable cyclostratigraphic data of Lantink et al. (2022).

The crucial importance of the stromatolite data at 1.88 Ga and 2.0 Ga used in previous models is an important motivation for the search for alternate estimates of the LOD in this time interval or more generally in the interval of 1.5 Ga to 2.0 Ga. A preference should be given to high resolution cyclostratigraphic data, in the spirit of Meyers and Malinverno (2018). In particular, it would be very useful to re-analyze the cyclostratigraphic data at 1.9 Ga of Grotzinger (1986). More generally, we would like here to emphasize the importance of taking dating (age) uncertainty into consideration when fitting variables through any type of empirical estimate derived from the geological records.

The two recent analytical, semi-analytical, and numerical studies of Wu et al. (2023) and Farhat et al. (2024), although providing opposite conclusions, have improved our understanding of the possibility of atmospheric thermotidal daylength locking in the Precambrian. The problem addressed in Wu et al. (2023) can be summarized as follows: two parameterized spectra of tidal torques, one gravitational and one thermal, are combined, and the parameters of the two counterparts are constrained such that the combined torque drives an LOD evolution that fits a compilation of geological proxies. Much can be appreciated in that work, especially in highlighting the significance of Earth-Moon angular momentum depletion via thermal tides, simulating the Lamb resonance for the Precambrian Earth using GCMs, and establishing a correlation between the resonant period, temperature evolution, and atmospheric compositional variations. Moreover, in the limited sense, the adopted analytical models of Wu et al. (2023), laying down the used spectra of the torques, appear to capture the fundamental dynamical behavior of oceanic and atmospheric tides. However, a closer look at the hierarchy of modeling assumptions in the two models and the constraints imposed by the geological proxies reveal that the story is much more nuanced. In short, stringent constraints on the LOD history were imposed by a subset of quantitatively questionable proxies, as we discuss in Section 2.1. The latter were combined with a spectrum of oceanic tides that does not physically describe the tidal response of the Earth’s paleo-oceans. As such, the modeled atmosphere was constrained to encounter the Lamb resonance with an unrealistic amplitude for the torque and in a whistle-stop fashion such that the stromatolite records in the Proterozoic can be explained.

Using a neutrally stratified analytical model that is more adapted to the Earth’s atmosphere than the usual isothermal model, and taking into account heat diffusion mechanisms in the vicinity of the ground interface, Farhat et al. (2024) conclude that the amplitude of the Lamb resonance is not sufficient for the thermotidal torque to counteract the luni-solar gravitational tidal torque when the crossing of the resonance occurs.

Interestingly, the numerical GCM simulations of Wu et al. (2023) allow to strengthen the analytical model of Farhat et al (2024) by probing the asymmetry of the Lamb resonance (Figure 7). These two studies should provide the basis of future improved models for atmospheric thermal tides, but for now, we should conclude, both by the consideration of the geological evidence and by the comparison of theoretical models, that there are no clear arguments supporting the hypothesis that LOD locking occurred in the past history of the Earth.

Acknowledgements

This project has been supported by the French Agence Nationale de la Recherche (AstroMeso ANR-19-CE31-0002-01) and by the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (Advanced Grant AstroGeo-885250). MLL acknowledges funding from the HeisingSimons grant no. 2021 – 2797.

Figures credits. Figure 3 from Mitchell and Kirscher (2023), Figures 3 and S4 from Wu et al. (2023), and Figure 11 from Bao et al. (2022) were adapted according to CC-BY licence (https://creativecommons.org/licenses/by/4.0/).

Conflict of interest

The authors declare having no conflict of interest.

Data availability

Data are available in the quoted references or on the AstroGeo website (www.astrogeo.eu).

Authors contribution

JL designed the study and made the first draft. JL, MF, ML, PAD, GB and MS contributed to the discussion of the work and writing of the paper.